Kishida, M.; Kusamoto, T.; Nishihara, H. J. Am. Chem. Soc., 2014, 136, 4809.
DOI: 10.1021/ja412528d
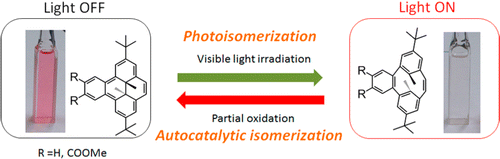
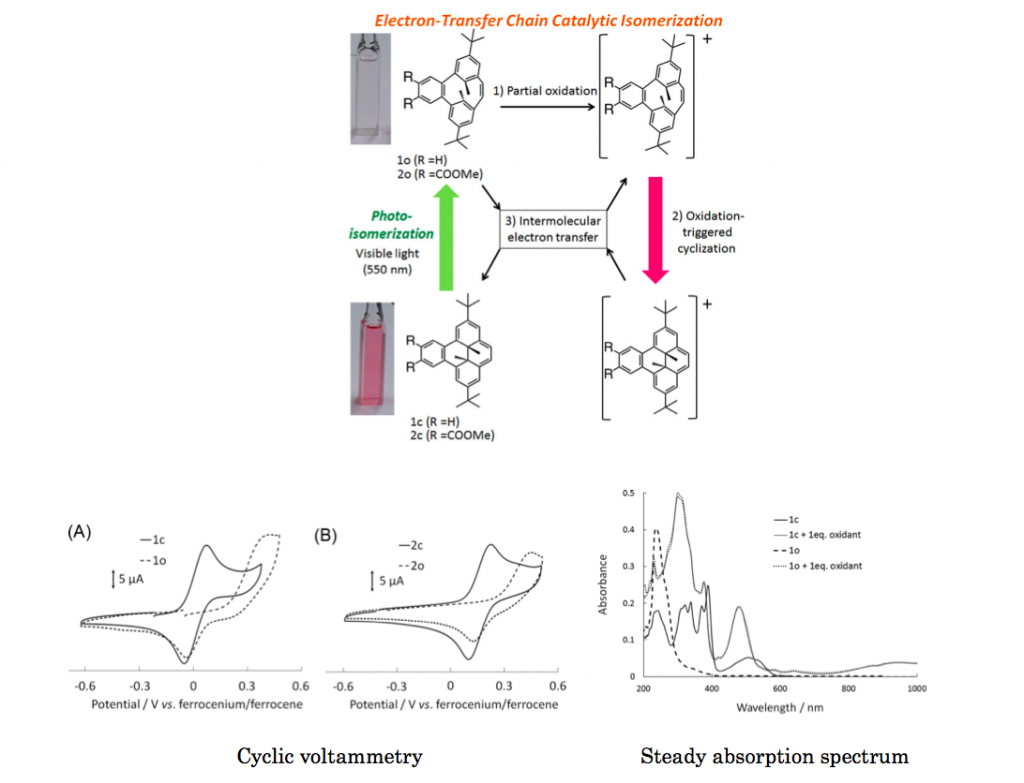
Photochromic benzocyclophanediene showed oxidation-triggered isomerization to form benzodimethyldihydropyrene. The isomerization proceeded via an autocatalytic reaction system, which could be combined with the photochromic nature of the molecule to establish a new photoelectric signal conversion system.
Introduction
IntroductionElectrochromism is a phenomenon where a specific type of molecule goes between two states reversibly by electronic stimuli. In fact, various photochromic compound shows electrochromic reaction, thus making photochromic molecule much more prominent in term of practical application like electronic devices.[1] Hiroshi Nishihara at Tokyo university reported autocatalytic reaction system of Benzodimethyldihydropyrene (BzDHP) which is one of very famous photochromic molecule.
Autocatalytic electrochromic reaction
Open ring form BzDHP does not absorb light in visible region hence appears to be transparent. After partial oxidation, O+ was instantly formed and readily converted to C+, passing original cation to neutral O to generate O+ again. The overall reaction cycle is completed by thermal isomerization from C to starting O. Additional experiments like cyclic voltammetry and steady absorption spectrum also suggest this proposed mechanism.[2]
Reference
[1]”Diarylethenes for Memories and Switches”
Irie, M. Chem. Rev. 2000, 100, 1685. DOI: 10.1021/cr980069d
[2]”Synthesis and Photochromic Properties of Molecules Containing [e]-Annelated Dihydropyrenes. Two and Three Way π-Switches Based on the Dimethyldihydropyrene−Metacyclophanediene Valence Isomerization”
Mitchell, R. H.; Ward, T. R.; Chen, Y.; Wang, Y.; Weerawarna, S. A.; Dibble, P. W.; Marsella, M. J.; Almutairi, A.; Wang, Z. J. Am. Chem. Soc. 2003, 125, 2974.
DOI: 10.1021/ja0288136