solvent isotope effect
An isotope effect that appears when a solvent labeled with an isotope (especially deuterium) is utilized.
In chemical research, there are many opportunities to investigate the physical properties and chemical reactions of molecules in heavy water (D2O) or heavy methanol (CD3OD) as substitutes for water or methanol using NMR or other means. In this case, the physical properties and reaction rates of the original molecule may change significantly in heavy solvents.
- Example 1: Acid Dissociation of Carboxylic Acids
The acid dissociation equilibrium constant of a carboxylic acid in D2O is smaller than in H2O, and the acid dissociation degree drops to about half.
- Example 2: Hydrolysis of Esters with Specific Acid Catalyst
The hydrolysis rate of esters with a specific acid catalyst (H3O+) can be about twice as fast in D2O as in H2O (inverse isotope effect).
Although the isotope effect of such solvents is less familiar than the kinetic isotope effect of deuterium labeling of substrates, it is important to note that the isotope effect may be more pronounced in heavy protic solvents. Since it is often easier to use deuterium-labeled solvents than to label complex substrates, this isotope effect is often used to analyze reaction mechanisms.
Based on a textbook [1], this article introduces the solvent isotope effect, focusing on the inverse isotope effect in the pre-equilibrium.
Concept of solvent isotope effect
- Fractionation factor
Given an equilibrium in which a molecule (substrate) SH with a certain protic hydrogen exchanges hydrogen isotopes with a deuterium-labeled alcohol solvent ROD, the equilibrium can be expressed as in the equation below:
(Note: The S in SH and SD stands for Substrate, not for Thiol.
Using the concentration of each substance in this equation, the fractionation factor φ is definedas in the following equation. [SD] denotes the concentration of SD.
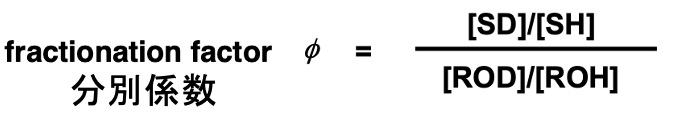
Fractionation factors can be measured experimentally and are useful for accurate prediction of isotope effects. The approximate value of the fractionation factors depends on the type of hydrogen bonding of each substrate (see figure below).[1]
These values are used to interpret and predict phenomena.
- Understanding Equilibrium
Assume that there is an equilibrium in which S’H arises from the substrate SH, and that a similar equilibrium exists for SD, where protic hydrogen is exchanged for deuterium.
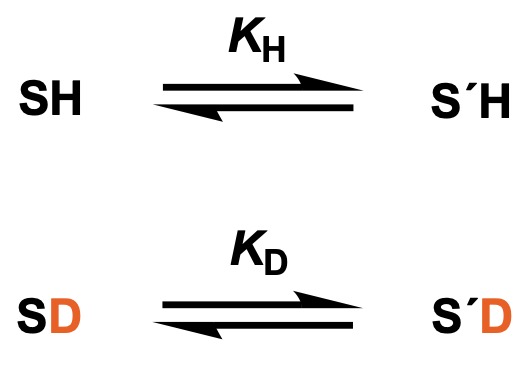Letting KH and KD be the equilibrium constants in the upper and lower equations, respectively, and φ and φ’ be the fractional factors for SH and S’H, KH/KD can be expressed as follows.
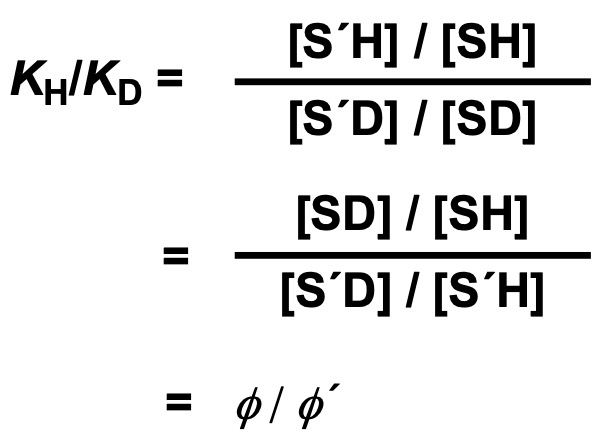Therefore, the equilibrium constant KD in the heavy solvent can be estimated by the equilibrium constant KH in the light solvent and the fractionation factors φ and φ’.
Interpretation of Example 1
Acid dissociation of carboxylic acids: The acid dissociation equilibrium constant of carboxylic acids in D2O is smaller than in H2O, and the acid dissociation degree drops to about half.
To predict this phenomenon, let us consider the following equilibrium, using acetic acid (CH3CO2H) as an example.
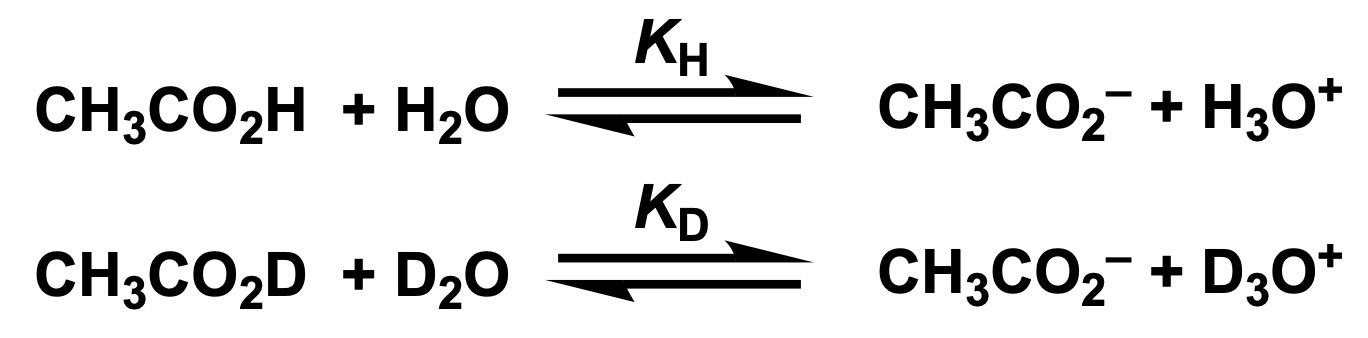
Each equilibrium constant is expressed in terms of the concentration of each substance:
Using these two equations to show KH/KD and replacing concentrations with the fractionation factors, we get:
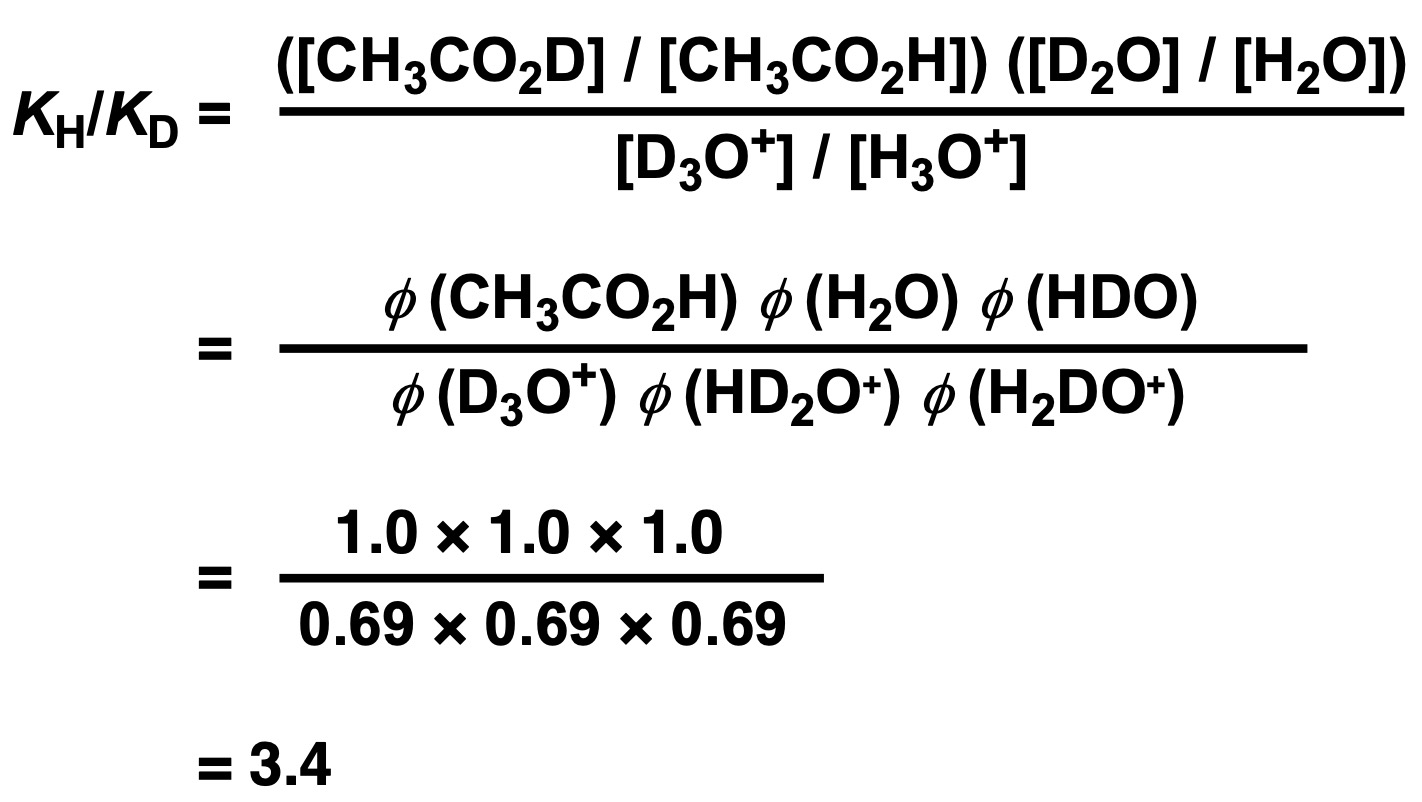
(Note that it takes two fractionation factors to link H2O and D2O (HDO, H2O) and three fractionation factors to link H3O+ and D3O+ (D3O+, HD2O+, H2DO+).
When the acid dissociation is small as in the case of acetic acid, the dissociation can be approximated as proportional to the square root of K. Therefore, it can be estimated that the dissociation in light water is 1.8 times greater than that in heavy water (= approximately half the dissociation in heavy water). Since the fractionation factor is similar for the ROH type, the same effect can be observed not only for carboxylic acids but also for alcohols. [2]
Interpretation of Example 2
Example 2: Hydrolysis of Esters with Specific Acid Catalyst
The hydrolysis rate of esters with a specific acid catalyst (H3O+) can be about twice as fast in D2O as in H2O (inverse isotope effect).
Consider SN1-type hydrolysis (e.g., ethyl benzoate). As shown in the equation below, the reaction proceeds in two steps, assuming equilibrium due to protonation (constant KH) and a rate-limiting step in which decomposition of the protonated product occurs (rate constant kR). The same equation can be formulated for heavy water. Using the fractionation factors, we can determine the isotope effect kH/kD on the overall rate of the reaction.
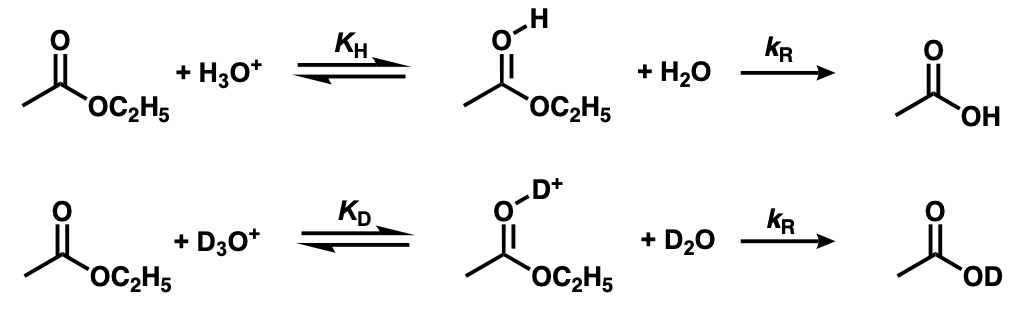The first equilibrium can be expressed as follows:
Assuming that no isotope effect appears in the rate-limiting step (kR), kH = KH × kR and kD = KD × kR . Using the above equation to express the isotope effect kH/kD and substituting concentrations with φ, we obtain kH/kD.
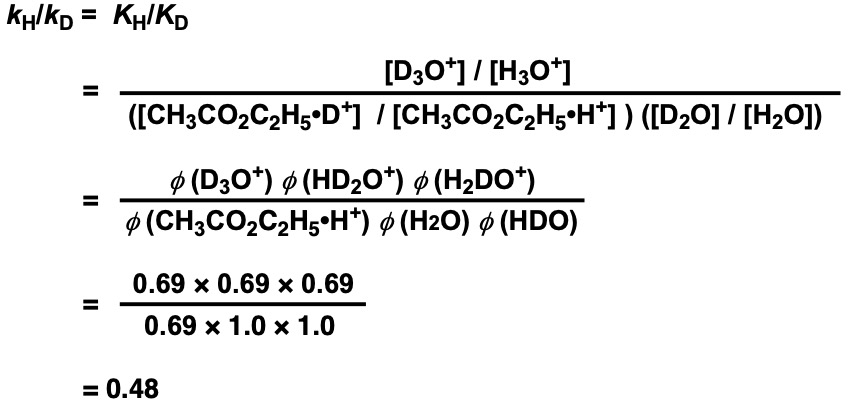
KIE = 0.48, which means that the hydrolysis reaction is approximately twice as fast in heavy water (inverse isotope effect).
The inverse isotope effect observed for Hofmann elimination of quaternary ammonium salts under basic conditions, which is seven times faster in heavy water, is also explained similarly. [3]
In contrast, in reactions where there is no pre-equilibrium and protonation is included in the rate-limiting step of the reaction, the primary isotope effect is significant and the reaction is slower in heavy water. A good example is the hydrolysis of vinyl ethers using carboxylic acids (general acid-catalyzed reaction). [1]
Extra: Kinetics
While the above isotope effects were observed in a system with a pre-equilibrium, the solvent KIE in the kinetic and rate-limiting phases can be considered in the same way. Consider the equation in which the substrate SH (starting material, sm) undergoes a transition state TS(H) (transition state, ts) to the product PH (product, pd). Let kH be the rate constant for this reaction. Similarly, for the deuterium-labeled substrate, consider the equation from SD through TS(D) to give PD. Let kD be the reaction rate constant for the deuterium-labeled substrate.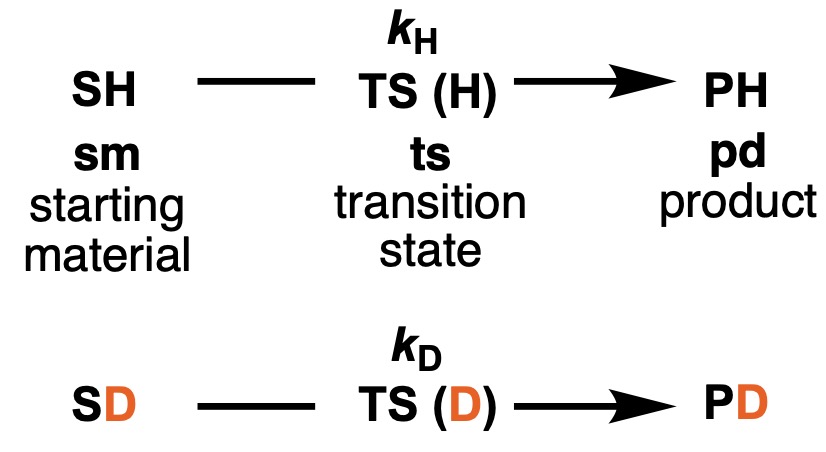
The kinetic isotope effect (KIE) can then be expressed as follows:
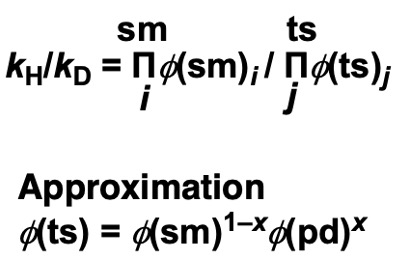
Note that the fractionation factors for the substrate and product can be measured, but not for the transition state. φ(ts) can be estimated as a weighted average, considering the transition state to be in between the two. (x is a measure of how close the transition state is to the product (0~1).
There are cases where (1) the molecule (substrate) has hydrogen that can be exchanged with the deuterated solvent (OH in alcohols, NH in amides, active methylene, etc.), (2) the catalyst has exchangeable hydrogen, and (3) the heavy solvent is directly involved in the reaction. In all cases where hydrogen transfer is included in the rate-limiting step of the overall reaction, the reaction is often slower in the heavy solvent. Even in these cases, evaluating the absolute value of KIE is tricky because inverse isotope effects can be involved when there is a pre-equilibrium in the reaction as in Example 2.
References
- 野依良治ほか編「大学院講義有機化学I(第一版)」東京化学同人, 1999.
- Albery, J. (1975). Solvent Isotope Effects. In: Caldin, E., Gold, V. (eds) Proton-Transfer Reactions. Springer, Boston, MA. https://doi.org/10.1007/978-1-4899-3013-2_9
- Clayden, Greeves, Warren, Organic Chemistry, 2nd eds. Oxford University Press, Chap 39, 2001.